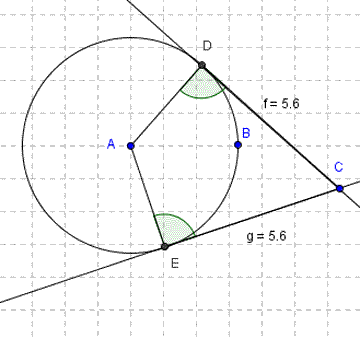
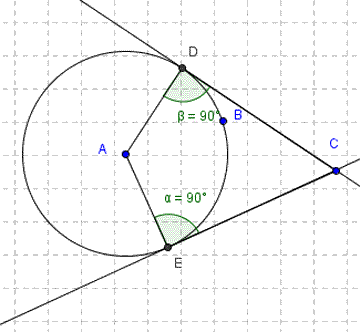
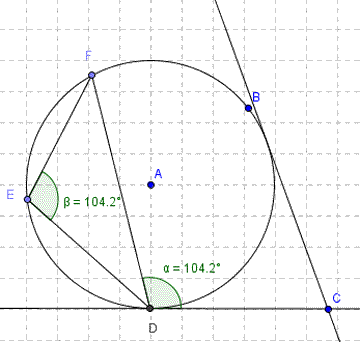
THEOREMS:
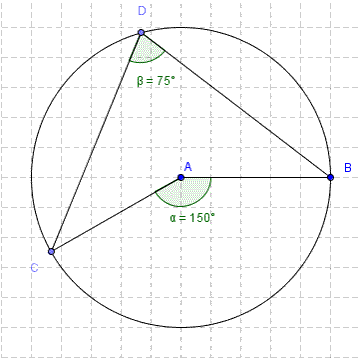
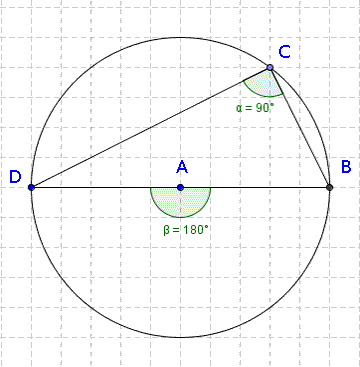
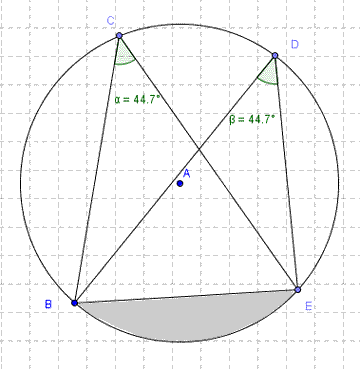
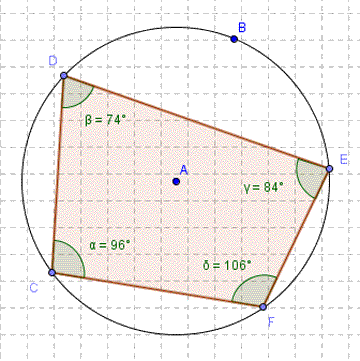
7. Alternate segment theorem:
Total Pageviews
Monday, 15 April 2013
MENSURATION FORMULAS
Mensuration Formulas
Mensuration is the branch of mathematics which deals with the study of Geometric shapes, their area, volume and related parameters.
Some important mensuration formulas are:
1. Area of rectangle (A) = length(l) × Breath(b)
2. Perimeter of a rectangle (P) = 2 × (Length(l) + Breath(b))
3. Area of a square (A) = Length (l) × Length (l)
4. Perimeter of a square (P) = 4 × Length (l)
5. Area of a parallelogram(A) = Length(l) × Height(h)

6. Perimeter of a parallelogram (P) = 2 × (length(l) + Breadth(b))
7. Area of a triangle (A) = (Base(b) × Height(b)) / 2

And for a triangle with sides measuring “a” , “b” and “c” , Perimeter = a+b+c
and s = semi perimeter = perimeter / 2 = (a+b+c)/2
And also: Area of triangle = 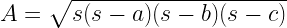
This formulas is also knows as “Heron’s formula”.
8. Area of triangle(A) = 1/2 ab sinC = 1/2 ac sinB = 1/2 bc sinA
Where A, B and C are the vertex and angle A , B , C are respective angles of triangles and a , b , c are the respective opposite sides of the angles as shown in figure below:

area of triangle - mensuration
9. Area of isosceles triangle = 
Where a = length of two equal side , b= length of base of isosceles triangle.
10. Area of trapezium (A) = 
Where “a” and “b” are the length of parallel sides and “h” is the perpendicular distance between “a” and “b” .

11. Perimeter of a trapezium (P) = sum of all sides
12. Area of rhombus (A) = Product of diagonals / 2
13. Perimeter of a rhombus (P) = 4 × l
where l = length of a side
14. Area of quadrilateral (A) = 1/2 × Diagonal × (Sum of offsets)

15. Area of a Kite (A) = 1/2 × product of it’s diagonals
16. Perimeter of a Kite (A) = 2 × Sum on non-adjacent sides
17. Area of a Circle (A) = 
Where r = radius of the circle and d = diameter of the circle.
18. Circumference of a Circle = 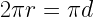
r= radius of circle
d= diameter of circle
19. Total surface area of cuboid = 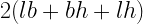
where l= length , b=breadth , h=height
20. Total surface area of cuboid = 
where l= length
21. length of diagonal of cuboid = 
22. length of diagonal of cube = √3 l
23. Volume of cuboid = l × b × h
24. Volume of cube = l × l × l
25. Area of base of a cone = 
26. Curved surface area of a cone = C = 
Where r = radius of base , l = slanting height of cone
27. Total surface area of a cone = 
28. Volume of right circular cone = 
Where r = radius of base of cone , h= height of the cone (perpendicular to base)
29. Surface area of triangular prism = (P × height) + (2 × area of triangle)
Where p = perimeter of base
30. Surface area of polygonal prism = (Perimeter of base × height ) + (Area of polygonal base × 2)
31. Lateral surface area of prism = Perimeter of base × height
32. Volume of Triangular prism = Area of the triangular base × height
33. Curved surface area of a cylinder = 
Where r = radius of base, h = height of cylinder
34. Total surface area of a cylinder = 
35. Volume of a cylinder = 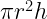
36. Surface area of sphere = 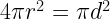
where r= radius of sphere, d= diameter of sphere
37. Volume of a sphere = 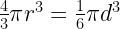
38. Volume of hollow cylinder = 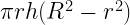
where , R = radius of cylinder , r= radius of hollow , h = height of cylinder
39. Right Square Pyramid:
If a = length of base , b= length of equal side ; of the isosceles triangle forming the slanting face , as shown in figure:

net diagram of right square pyramid
39.a Surface area of a right square pyramid = 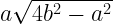
39.b Volume of a right square pyramid = 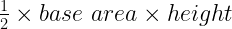
40. Square Pyramid:
40.a. Johnson Pyramid:

- net diagram of johnson pyramid
Volume = 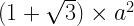
Total Surface Area: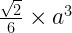
Total Surface Area:
40.b. Normal Square pyramid:
If a = length of square base and h = height of the pyramid then:
Volume =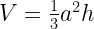
Total Surface Area =
Volume =
Total Surface Area =
41. Area of a regular hexagon = 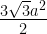
42. area of equilateral triangle = 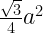
43. Curved surface area of a Frustums =  (h = lateral height)
(h = lateral height)
44. Total surface area of a Frustums = 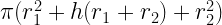 (h= lateral height)
(h= lateral height)
45. Curved surface area of a Hemisphere = 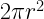
46. Total surface area of a Hemisphere = 
47. Volume of a Hemisphere = 
48. Area of sector of a circle = 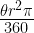
where  = measure of angle of the sector , r= radius of the sector
= measure of angle of the sector , r= radius of the sector
Subscribe to:
Posts (Atom)